Back to basics: PCA on stocks returns

A short code snippet to apply PCA on stocks returns. No secret sauce is used here to clean the empirical covariance matrix. This blog post will mostly serve as a basis for comparing several flavours of PCA and their impact on ex-ante volatility estimation. We may look in future blog posts into Sparse PCA, Nonlinear PCA, Kernel PCA, Robust PCA, revisit our previous implementation of Hierarchical PCA (HPCA), and other techniques such as Independent Component Analysis (ICA).

from pathlib import Path
from datetime import datetime
import numpy as np
import pandas as pd
from tqdm import tqdm
from pandas.tseries.offsets import BDay
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt

sp500 = pd.read_csv('SP500_HistoTimeSeries.csv', 
                    index_col='Date',
                    date_parser=lambda x: datetime.strptime(x, '%d/%m/%Y'))
sp500.index = pd.to_datetime(sp500.index)
sp500 = sp500.sort_index()
returns = sp500.pct_change()
returns = returns.clip(lower=-0.25, upper=0.25)
del returns['SPX Index']

NB_EIGEN = 5
LOOKBACK_WINDOW = 2 * 252

dates = returns.index[LOOKBACK_WINDOW:]

factor_covariances = []
factor_exposures = []
residual_vols = []

for date in tqdm(dates):
    # compute the PCA on rolling past returns
    past_returns = returns.loc[date - BDay(LOOKBACK_WINDOW):date]
    past_returns = past_returns[(past_returns.count() > 100)
                                .replace(False, np.nan)
                                .dropna()
                                .index]
    cov = past_returns.cov()
    eig_vals, eig_vecs = np.linalg.eig(cov)
    permutation = np.argsort(-eig_vals)
    eig_vals = eig_vals[permutation]
    eig_vecs = eig_vecs[:, permutation]
    zeroed_returns = past_returns.replace(np.nan, 0)
    factors = zeroed_returns @ eig_vecs.real
    factors_5 = factors.iloc[:, :NB_EIGEN]
    reg = (LinearRegression(fit_intercept=True)
           .fit(X=factors_5, y=past_returns.fillna(0)))
    B = reg.coef_
    pca_returns = reg.predict(factors_5)
    resid = past_returns - pca_returns
    resid_vol = resid.std()
    D = np.diag(resid_vol)**2
    
    # factor covariance
    fCov = (factors_5
            .cov()
            .rename(columns={i: 'E' + str(i) for i in range(NB_EIGEN)},
                    index={i: 'E' + str(i) for i in range(NB_EIGEN)})
            .stack()
            .reset_index()
            .rename(columns={'level_0': 'factor_1',
                             'level_1': 'factor_2',
                             0: 'covar'}))
    fCov['date'] = date
    fCov = fCov.set_index(['date', 'factor_1', 'factor_2'])
    
    # factor exposures
    fExp = pd.DataFrame(B,
                        index=past_returns.columns,
                        columns=['E' + str(i) for i in range(NB_EIGEN)])
    fExp['date'] = date
    fExp = fExp.reset_index().rename(columns={'index': 'ticker'})
    fExp = fExp.set_index(['date', 'ticker'])
    
    # specific risk
    spec_risk = (resid_vol
                 .reset_index()
                 .rename(columns={'index': 'ticker',
                                  0: 'resid_vol'}))
    spec_risk['date'] = date
    spec_risk = spec_risk.set_index(['date', 'ticker'])
    
    # save the factor covariance, exposures, and stocks specific risk
    factor_covariances.append(fCov)
    factor_exposures.append(fExp)
    residual_vols.append(spec_risk)
    
factor_covariances = pd.concat(factor_covariances)
factor_exposures = pd.concat(factor_exposures)
residual_vols = pd.concat(residual_vols)

100%|██████████| 3470/3470 [24:27<00:00,  2.37it/s]

We save the factors covariance, exposures, and residual volatilities for future reuse:

Path("risk_model").mkdir(parents=True, exist_ok=True)
factor_covariances.to_parquet('risk_model/factor_covariances.parquet')
factor_exposures.to_parquet('risk_model/factor_exposures.parquet')
residual_vols.to_parquet('risk_model/residual_vols.parquet')

Loading the saved risk model components:

factor_covariances = pd.read_parquet('risk_model/factor_covariances.parquet')
factor_exposures = pd.read_parquet('risk_model/factor_exposures.parquet')
residual_vols = pd.read_parquet('risk_model/residual_vols.parquet')

factor_covariances.tail()

			covar
date	factor_1	factor_2
2016-07-29	E4	E0	-0.000842
		E1	0.000078
		E2	0.000133
		E3	-0.000007
		E4	0.002611

factor_exposures.tail()

		E0	E1	E2	E3	E4
date	ticker
2016-07-29	XEC UN Equity	0.068088	-0.108401	0.040181	0.003394	-0.173384
	ZTS UN Equity	0.037352	0.036895	-0.015819	-0.090589	-0.037028
	DLR UN Equity	0.019566	0.026160	0.081157	0.001729	0.017967
	EQIX UW Equity	0.034544	0.045924	0.033238	-0.006657	-0.018939
	DISCK UW Equity	0.052699	-0.012641	0.002077	0.010083	0.039095

residual_vols.tail()

		resid_vol
date	ticker
2016-07-29	XEC UN Equity	0.012693
	ZTS UN Equity	0.013028
	DLR UN Equity	0.009801
	EQIX UW Equity	0.011945
	DISCK UW Equity	0.014904

We now apply the risk model through history on a long-only equally weighted portfolio:

backtest_dates = sorted(residual_vols.index.get_level_values(0).unique())

# long-only equally weighted portfolio
weights = pd.DataFrame(False, index=returns.index, columns=returns.columns)

for date in tqdm(backtest_dates):
    weights.loc[date, residual_vols.loc[date, :].index] = True

weights = weights.astype(int)
weights = (weights
           .div(weights.sum(axis=1), axis=0)
           .replace(0, np.nan))

100%|██████████| 3470/3470 [02:30<00:00, 23.05it/s]

rets = (weights * returns.shift(-1)).sum(axis=1).loc[backtest_dates]
realized_vol = rets.rolling(63).std()

rets.cumsum().plot(
    title=f"Sharpe: {round(rets.mean() * np.sqrt(252) / rets.std(), 2)}")
plt.show()

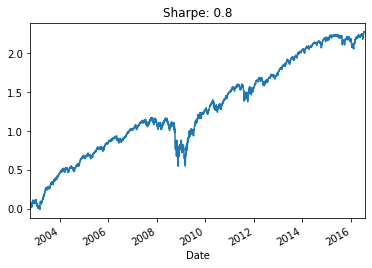
performance of the long-only portfolio
Performance and Sharpe ratio of the equally weighted long-only portfolio

pca_risk = []
for date in tqdm(backtest_dates):
    w = weights.loc[date].dropna()
    r = residual_vols.loc[date, :]
    e = factor_exposures.loc[date, :]
    c = (factor_covariances
         .loc[date, :, :]
         .reset_index()
         .pivot(index='factor_1',
                columns='factor_2',
                values='covar'))
    cov = e @ c @ e.T + np.diag(r.resid_vol**2)
    risk =  np.sqrt(w.T @ cov @ w)
    pca_risk.append(risk)
    
pca_risk = pd.Series(pca_risk, index=backtest_dates)

100%|██████████| 3470/3470 [01:03<00:00, 54.44it/s]

(pca_risk * np.sqrt(252)).plot( label='2y-PCA model risk')
(realized_vol * np.sqrt(252)).plot(label='3m realized risk')
plt.legend()
plt.show()

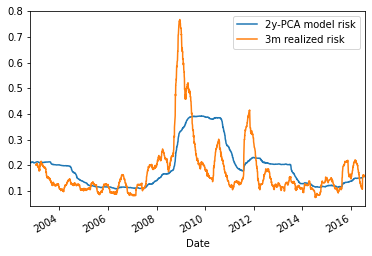
realized vol and ex-ante risk model vol
time series of the 3-month realized volatility (orange), and the *ex-ante* volatility (blue) given by the 2-year 5-factor PCA risk model

On average the 5-factor PCA risk model overestimates the risk by 5%:

(realized_vol / pca_risk).plot()
round((realized_vol / pca_risk).mean(), 2)

0.95

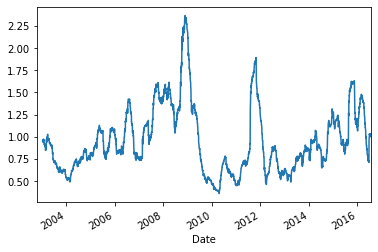
realized vol over ex-ante risk model vol
time series of the ratio between 3-month realized volatility over *ex-ante* volatility given by the 2-year 5-factor PCA risk model

We can see on the graph above that the 5-factor PCA risk model applied to such a simple long-only portfolio can be off by a factor 2 in case of extreme vol in the markets. Following a crisis, the risk model will be too conservative for a while… The duration of that period matches roughly the window length used for the PCA calibration (i.e. the rolling window size used to estimate the covariance between the stocks returns).